いろいろな言語での関数, 手続き, サブルーチンの例
Riemann
zeta 関数
$\displaystyle{\zeta(s)=\sum_{k=1}^\infty \frac{1}{k^s}}$
を素朴に近似計算
C言語版
これをファイル myzeta.c に貼り付けて保存. コンパイル, 実行は
cc myzeta.c -lm
./a.out
python 版
これをファイル myzeta.py に貼り付けて保存. インタプリタによる実行は
python <myzeta.py
または
python3 <myzeta.py
ファイルの入力間違いなどで強制終了したいときは ctrl-C
Java 版
これをファイル myzeta.java に貼り付けて保存. コンパイル, 実行は
javac myzeta.java
java myzeta
R版
これをファイル myzeta.r に貼り付けて保存. インタプリタによる実行は
R --no-save <myzeta.r
R では R を起動したあと
source("myzeta.r");
で実行する方法の方がよく使われる.
数学ソフトウエアでは zeta 関数の計算はあらかじめ組み込まれている
- Maxima (maxima でインタプリタがスタート)
bfzeta(3,5);
s=3 で 5 の部分は小数点以下の桁数
- Risa/Asir (openxm asir でインタプリタがスタート)
setprec(100);
pari(zeta,3);
setprec で欲しい桁数を指定.
- Mathematica (購入が必要)
N[Zeta[3],100]
100 桁の近似値.
- Sage math (sage でインタプリタがスタート)
zeta(3).n(digits=100)
などなど.
Euler 積表示での値と比べる
Euler 積とは
$\displaystyle{ \zeta(s)=\prod_{p: \mbox{prime number}}
\left(\frac{1}{1-\frac{1}{p^s}} \right)
}$
python 版
sympy ライブラリをまずインストール.
- python3 では
sudo apt install python3-sympy
- python2 では
sudo apt install python-sympy
- apt でインストールできない時は
pip install sympy
か
pip3 install sympy
このプログラムを myzeta2.py へ貼り付けて保存. インタプリタで次のように実行.
python <myzeta2.py
または
python3 <myzeta2.py
Risa/Asir 版
このプログラムを myzeta2.rr へ貼り付けて保存. インタプリタでの実行は
openxm asir <myzeta2.rr
なおファイルの入力間違いなどで強制終了したいときは ctrl-C でなく,
ctrl-Z
それから kill %%
asir ではプログラム中から
load("myzeta2.rr");
で実行する方法の方がよく使われる.
Mathematica による zeta 関数のグラフ
s の実部を 1/2, 虚部を [0,50] で動かす.
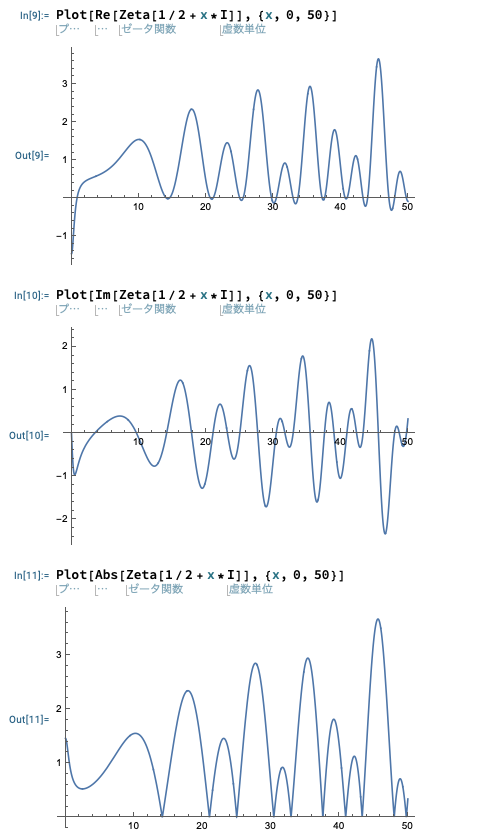
参考: zeta 関数の効率的数値計算法
-
大島利雄, 自然数の負の奇数ベキの無限和の収束とその誤差 ,
$\zeta(奇数)$ の初等的高速計算法.
- stack exchange の記事 (専門的).
-
Ghaith Ayesh Hiary, Fast methods to compute the Riemann zeta function
(2011)
,
専門論文の例.
