Examples: gb, rrank, gkz, bfunction, deRham

Execute Loadall to load packages before executing examples. Dx means $\partial_x$.

Example 1   Compute a Gröbner basis and the initial ideal with respect to the weight vector $(0,0,1,1)$ of the $D$-ideal

$$D \cdot \{ (x \partial_x)^2 + (y \partial_y)^2 -1, x y \partial_x \partial_y-1 \}.$$

See [5] on the notion of Gröbner basis and the initial ideal with respect to a weight vector.

 [ [( (x Dx)^2 + (y Dy)^2 -1) ( x y Dx Dy -1)] (x,y) 
             [ [ (Dx) 1 (Dy) 1] ] ] gb pmat ;

Output:

 [ 
  [ x^2*Dx^2+y^2*Dy^2+x*Dx+y*Dy-1 , x*y*Dx*Dy-1 , y^3*Dy^3+3*y^2*Dy^2+x*Dx ] 
  [ x^2*Dx^2+y^2*Dy^2 , x*y*Dx*Dy , y^3*Dy^3 ] 
 ]

The first line is the Gröbner basis and the second line is a set of generators of the initial ideal with respect to the weight vector $(0,0,1,1)$. In order to get syzygies, use syz.

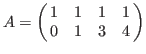Example 2   Generate the GKZ system for $A=\pmatrix{1 & 1 & 1 & 1 \cr 0 & 1 & 3 & 4 \cr}$ and $\beta = (1,2)$. Here, the GKZ system is a holonomic system of differential equations introduced by Gel'fand, Kapranov and Zelevinsky. The system is also called ${\cal A}$-hypergeometric system.

   [ [[1 1 1 1] [0 1 3 4]] [1 2]] gkz  ::

Output:

 [ x1*Dx1+x2*Dx2+x3*Dx3+x4*Dx4-1 , x2*Dx2+3*x3*Dx3+4*x4*Dx4-2 , 
   Dx2*Dx3-Dx1*Dx4 , -Dx1*Dx3^2+Dx2^2*Dx4 , Dx2^3-Dx1^2*Dx3 , 
   -Dx3^3+Dx2*Dx4^2 ]

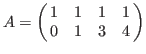Example 3   Evaluate the holonomic rank of the GKZ systems for $A=\pmatrix{1 & 1 & 1 & 1 \cr 0 & 1 & 3 & 4 \cr}$ and $\beta = (1,2)$ and $\beta=(0,0)$. Show also the time of the execution.

  { [ [[1 1 1 1] [0 1 3 4]] [1 2]] gkz  rrank ::} timer
  { [ [[1 1 1 1] [0 1 3 4]] [0 0]] gkz  rrank ::} timer

Output:

   5
User time: 1.000000 seconds, System time: 0.010000 seconds, Real time: 1 s
   4
User time: 1.320000 seconds, System time: 0.000000 seconds, Real time: 1 s

Example 4   Compute the $b$-function of $f=x^3-y^2 z^2$ and the annihilating ideal of $f^{r_0}$ where $r_0$ is the minimal integral root of the $b$-function.

   (oxasir.sm1) run
   [(x^3 - y^2 z^2) (x,y,z)] annfs /ff set
   ff message
   ff 1 get 1 get fctr ::

Output:

[  [ -y*Dy+z*Dz , 2*x*Dx+3*y*Dy+6 , -2*y*z^2*Dx-3*x^2*Dy , 
   -2*y^2*z*Dx-3*x^2*Dz , -2*z^3*Dx*Dz-3*x^2*Dy^2-2*z^2*Dx ]  , 
 [-1,-139968*s^7-1119744*s^6-3802464*s^5-7107264*s^4-7898796*s^3-5220720*s^2-1900500*s-294000]] 
[[ -12 , 1 ] , [ s+1 , 1 ], [3*s+5 , 1], [ 3*s+4, 1], [6*s+7, 2], [6*s+5, 2]]

The first two rows of the output give generators of the annihilating ideal of $(x^3-y^2 z^2)^{-1}$. The $b$-function is $(s+1)(3s+5)(3s+4)(6s+7)^2(6s+5)^2$ and $-1$ is the minimal integral root.

Example 5   Compute the de Rham cohomology group of $X={\bf C}^2 \setminus V(x^3-y^2)$.

    (cohom.sm1) run
    [(x^3-y^2) (x,y)] deRham ;

Output:

  0-th cohomology:  [    0 , [   ]  ] 
  -1-th cohomology:  [    1 , [   ]  ] 
  -2-th cohomology:  [    1 , [   ]  ] 
 [1 , 1 , 0 ]

This means that $H^2(X,{\bf C}) = 0$, $H^1(X,{\bf C}) = {\bf C}^1$, $H^0(X,{\bf C}) = {\bf C}^1$.

Example 6   Compute the integral of $I=D\cdot \{\partial_t -(3 t^2-x) ,\, \partial_x+t \}$, which annihilates the function $e^{t^3-x t}$, with respect to $t$.

 (cohom.sm1) run
 [ [(Dt - (3 t^2-x)) (Dx + t)] [(t)]
   [ [(t) (x)] [ ]] 0] integration

Output:

[    [    1 , [    3*Dx^2-x ]  ]  ]