1077 functions are available on our servers and libraries

$\fbox{\huge {\color{green} $D$-modules}}$ ( is the Weyl algebra)

gb (Gröbner basis), syz (syzygy), annfs (Annhilating ideal of ), bfunction, schreyer (free resolution by the Schreyer method), vMinRes (V-minimal free resolution), characteristic (Characteristic variety), restriction in the derived category of -modules, integration in the derived category, tensor in the derived category, dual (Dual as a D-module), slope.

$\fbox{\huge {\color{green} Cohomology groups}}$

deRham (The de Rham cohomology groups of ${\bf C}^n \setminus V(f)$ , ext (Ext modules for a holonomic -module and the ring of formal power series).

$\fbox{\huge {\color{green} Differential equations}}$

Helping to derive and prove combinatorial and special function identities, gkz (GKZ hypergeometric differential equations), appell (Appell's hypergeometric differential equations), indicial (indicial equations), rank (Holonomic rank), rrank (Holonomic rank of regular holonomic systems), dsolv (series solutions of holonomic systems).

$\fbox{\huge {\color{green} OpenMATH support}}$

om_xml (CMO to OpenMATH XML), om_xml_to_cmo (OpenMATH XML to CMO).

$\fbox{\huge {\color{green} Homotopy Method}}$

phc (Solving systems of algebraic equations by numerical and polyhedral homotopy methods).

$\fbox{\huge {\color{green} Toric ideal}}$

tigers (Enumerate all Gröbner basis of a toric ideal. Finding test sets for integer program), arithDeg (Arithmetic degree of a monomial ideal), stdPair (Standard pair decomposition of a monomial ideal).

$\fbox{\huge {\color{green} Communications}}$

ox_launch (starting a server), ox_launch_nox, ox_shutdown, ox_launch_generic, generate_port, try_bind_listen, try_connect, try_accept, register_server, ox_rpc, ox_cmo_rpc, ox_execute_string, ox_reset (reset the server), ox_intr, register_handler, ox_push_cmo, ox_push_local, ox_pop_cmo, ox_pop_local, ox_push_cmd, ox_sync, ox_get, ox_pops, ox_select, ox_flush, ox_get_serverinfo

In addition to these functions, Mathematica functions can be called as server functions. $\fbox{\huge {\color{green} Examples}}$

[345] sm1_deRham([x^3-y^2*z^2,[x,y,z]]);
[1,1,0,0]
/* dim H^i = 1 (i=0,1), =0 (i=2,3) */

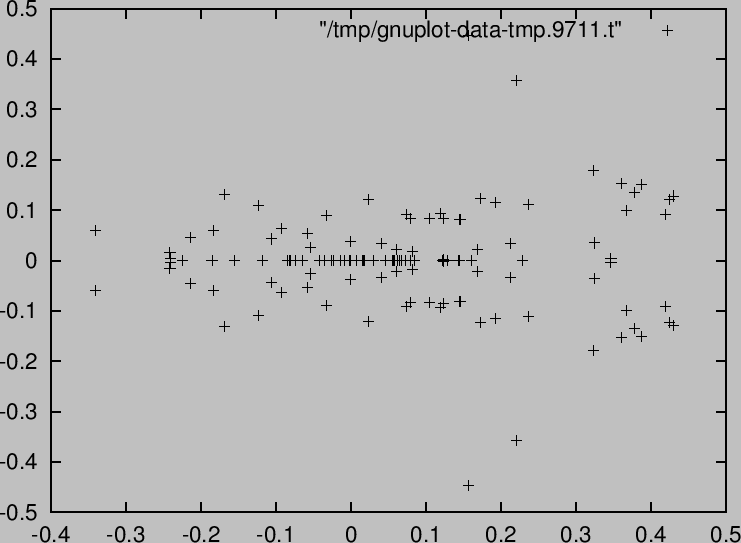
[287] phc(katsura(7)); B=map(first,Phc)$
[291] gnuplot_plotDots(B,0)$

=3cm

$\epsffile{katsura7.ps}$

$\fbox{ {\color{green} Authors}}$ Castro-Jiménez, Dolzmann, Hubert, Murao, Noro, Oaku, Okutani, Shimoyama, Sturm, Takayama, Tamura, Verschelde, Yokoyama.

http://www.openxm.org

About this document ...

Nobuki Takayama 2017-03-30