As Schefström clarified in [17],
integration of tools and software has three dimensions:
data, control, and user interface.
Data integration concerns with the exchange of data between different
software or same software.
OpenMath [1] and MP (Multi Protocol) [3] are,
for example, general purpose mathematical data protocols.
They provide standard ways to express mathematical objects.
For example,
<OMOBJ> <OMI> 123 </OMI> </OMOBJ>
means the (OpenMath) integer 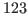 in OpenMath/XML expression.
in OpenMath/XML expression.
Control integration concerns with the establishment and management of
inter-software communications.
Control involves, for example, a way to ask computations to other processes
and a method to interrupt computations on servers from a client.
RPC, HTTP, MPI, PVM are regarded as a general purpose control protocols or
infrastructures.
MCP (Mathematical Communication Protocol)
by Wang [21] is such a protocol for mathematics.
Although data and control are orthogonal to each other,
real world requires both.
NetSolve [9], OpenMath MCP, MP
MCP, MP MCP [21],
and MathLink [22] provide both data and control integration.
Each integration method has their own features determined by their
own design goals.
OpenXM (Open message eXchange protocol for Mathematics)
is a project aiming to integrate data, control and user interfaces
with design goals motivated by the followings.
MCP [21],
and MathLink [22] provide both data and control integration.
Each integration method has their own features determined by their
own design goals.
OpenXM (Open message eXchange protocol for Mathematics)
is a project aiming to integrate data, control and user interfaces
with design goals motivated by the followings.
- The proposed standards mentioned above such as OpenMath
should be tested on various mathematical software systems,
but the testing has not been enough in comparison with
internet protocols.
- Noro has been involved in the development of
a computer algebra system Risa/Asir [10].
An interface for interactive distributed computations was introduced
to Risa/Asir in 1995.
The model of computation was RPC (remote procedure call).
A robust interruption protocol was provided
by two communication channels
like the File Transfer Protocol (ftp).
As an application of this protocol,
a parallel speed-up was achieved for a Gröbner basis computation
to determine all odd order replicable functions
(Noro and McKay [11]).
However, the protocol was local in Asir and we thought that we should
design an open protocol.
- Takayama has developed
a special purpose system Kan/sm1 [19],
which is a Gröbner engine for the ring of differential operators
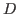 .
In order to implement algorithms in
.
In order to implement algorithms in 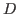 -modules due to Oaku
(see, e.g., [16]),
factorizations and primary ideal decompositions are necessary.
Kan/sm1 does not have an implementation for these and called
Risa/Asir as a UNIX external program.
This approach was not satisfactory.
Especially, we could not write a clean interface code between these
two systems.
We thought that it is necessary to provide a data and control protocol
for Risa/Asir to work as a server of factorization and primary ideal
decomposition.
-modules due to Oaku
(see, e.g., [16]),
factorizations and primary ideal decompositions are necessary.
Kan/sm1 does not have an implementation for these and called
Risa/Asir as a UNIX external program.
This approach was not satisfactory.
Especially, we could not write a clean interface code between these
two systems.
We thought that it is necessary to provide a data and control protocol
for Risa/Asir to work as a server of factorization and primary ideal
decomposition.
- We have been profited from increasing number
of mathematical software.
These are usually ``expert'' systems in one area of mathematics
such as ideals, groups, numbers, polytopes, and so on.
They have their own interfaces and data formats,
which are fine for intensive users of these systems.
However, a unified system will be more convenient
for users who want to explore a new area of mathematics with these
software or users who need these systems only occasionally.
- We believe that an open integrated system is a future of mathematical
software.
However, it might be just a dream without realizability.
We want to build a prototype of such an open system by using
existing standards, technologies and several mathematical software.
We want to see how far we can go with this approach.
Motivated with these, we started the OpenXM project with the following
fundamental architecture, which is currently described in
OpenXM-RFC 100 proposed standard
``Design and Implementation of OpenXM client-server model and common
mathematical object format'' [12].
- Communication is an exchange of messages. The messages are classified into
three types:
DATA, COMMAND, and SPECIAL.
They are called OX (OpenXM) messages.
Among the three types,
OX data messages wrap mathematical data.
We use standards of mathematical data formats such as OpenMath and MP
as well as our own data format CMO
(Common Mathematical Object format),
which can be expressed in terms of XML.
- Servers, which provide services to other processes, are stack machines.
The stack machine is called the
OX stack machine.
Existing mathematical software systems are wrapped with this stack machine.
Minimal requirements for a target software wrapped with the OX stack machine
are as follows:
- The target must have a serialized interface such as a character based
interface.
- An output of the target must be understandable for computer programs;
it should follow a grammar that can be parsed with other software.
- Any server may have a hybrid interface;
it may accept and execute not only stack machine commands,
but also its original command sequences.
For example,
if we send the following string to the ox_asir server
(OpenXM server of Risa/Asir)
" fctr(x^100-y^100); "
and call the stack machine command
SM_executeStringByLocalParser
then the server executes the asir command
fctr(x^100-y^100);
(factorize
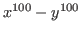 over
over 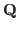 )
and pushes the result onto the stack.
)
and pushes the result onto the stack.
OpenXM package implements the OpenXM-RFC 100 [12]
and 101 [14] based on
the above fundamental architecture.
In this paper, we discuss mainly on systems implementing
OpenXM-RFC 100 and 101 on TCP/IP.
For example, the following is a command sequence to ask 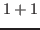 from
the Asir client to the ox_sm1 server through TCP/IP:
from
the Asir client to the ox_sm1 server through TCP/IP:
P = sm1_start();
ox_push_cmo(P,1); ox_push_cmo(P,1);
ox_execute_string(P,"add"); ox_pop_cmo(P);
Here, ox_sm1 is an OpenXM server of Kan/sm1.
Our project of integrating mathematical software
systems is taking the ``RFC'' approach, which has been
used to develop internet protocols.
We think that ``RFC'' approach is an excellent way and
we hope that other groups, who are working on standard protocols,
take this ``RFC'' approach, too.
The OpenXM on MPI [8] is currently running on Risa/Asir
as we will see in Section 9.2.
We are now preparing the OpenXM-RFC 102 ``Mathematical communication
on MPI'' (draft protocol)
based on our experiments on MPI.
In the rest of the paper, we abbreviate
OpenXM-RFC 100 and 101 to OpenXM if no confusion arises.
Nobuki Takayama
2017-03-30
![]() MCP, MP
MCP, MP![]() MCP [21],
and MathLink [22] provide both data and control integration.
Each integration method has their own features determined by their
own design goals.
OpenXM (Open message eXchange protocol for Mathematics)
is a project aiming to integrate data, control and user interfaces
with design goals motivated by the followings.
MCP [21],
and MathLink [22] provide both data and control integration.
Each integration method has their own features determined by their
own design goals.
OpenXM (Open message eXchange protocol for Mathematics)
is a project aiming to integrate data, control and user interfaces
with design goals motivated by the followings.