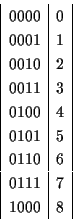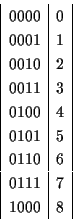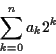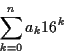2 進数と 16 進数

計算機の扱える情報は 2 進数である. それらにたいする, 四則演算と記憶ですべてのことが すすむ. これを常に念頭において以下勉強していくのが, 理解の早道であろう.

2進数で 8 桁の情報を 1 byte とよぶ. メモリは各番地に 1 byte の情報を格納できる. 2進数は 0 と 1 の 2 つの記号を用いて数を表現する. 2進数と 10進数の対応は以下のとおり.

$$\begin{array}{\vert c\vert c\vert} 0000 & 0 \\ 0001 & 1 \... ...1 & 5 \\ 0110 & 6 \\ 0111 & 7 \\ 1000 & 8 \\ \end{array}$$

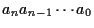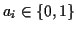$a_n a_{n-1} \cdots a_0$, $a_i \in \{0, 1\}$ なる 表示の 2進数を 10進数であらわすと,

$$\sum_{k=0}^n a_k 2^k$$

に等しい. たとえば, 2進数 1101 は, 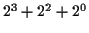$2^3 + 2^2 + 2^0$ に等しい.

2 進数を書くのは桁が多くて面倒なので, 代わりに 普通 16 進数を使うことが多い. 16 進数 2 桁が 2 進数 8 桁に対応するので換算が簡単である. 16 進数では

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

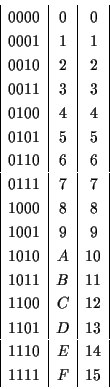
と 16個の記号を用いて数をあらわす. A が 10進数の 10, B が 10進数の 11, C が 10進数の 12, D が 10進数の 13, E が 10進数の 14, F が 10進数の 15 に対応する. したがって, 2進数, 16進数, 10進数の対応は以下のようになる.

$$\begin{array}{\vert c\vert c\vert c\vert} 0000 & 0 & 0 \\ ... ... & D & 13 \\ 1110 & E & 14 \\ 1111 & F & 15 \\ \end{array}$$

    

$$\begin{array}{\vert c\vert c\vert c\vert} 10000 & 10 & 16 \... ... & 29 \\ 11110 & 1E & 30 \\ 11111 & 1F & 31 \\ \end{array}$$

16 進数は 0x や H をつけて表すことも多い. また A から F を小文字で書くことも多い. たとえば 0x1E, 0x1e, 1EH, 1eH はすべて 16進数の 1E を表す. 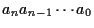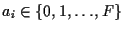$a_n a_{n-1} \cdots a_0$, $a_i \in \{0, 1, \ldots, F\}$ なる 表示の 16進数を 10進数であらわすと,

$$\sum_{k=0}^n a_k 16^k$$

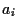に等しい. ただし $a_i$ が 0xA のときは 10, 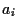$a_i$ が 0xB のときは 11, 等と解釈する. 2 進数と 16 進数の間の変換は容易であろう.

練習 4.1   次の 16 進数達を 10 進数, 2 進数で書け. 0xFF, 0x100, 0xFFFF, 0x10000, 0x81.

練習 4.2   16 進数で筆算をやることを試みよ.

計算機が数を有限桁の 2 進数で表現していることを 実感する例として次の計算をやってみるのはおもしろいであろう.

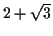
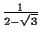
例題 4.1   $2 + \sqrt{3}$ と $\frac{1}{2-\sqrt{3}}$ の近似値を JavaScript で計算してみなさい.

<script language="JavaScript">
   document.write(2+Math.sqrt(3),"<BR>");
   document.write(1/(2-Math.sqrt(3)));
</script>

結果は次のようになる.

3.732050807568877
3.732050807568876

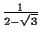
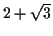
$\frac{1}{2-\sqrt{3}}$ の分母を有理化すると $2 + \sqrt{3}$ に等しいはずだが, 近似的な数値計算では このように誤差が生じる.