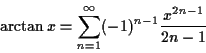効率的なプログラムを書くには?

例として $e = \sum_{i=0}^\infty 1/i!$ を部分和で近似することを考える. $e(N) = \sum_{i=0}^N 1/i!$ とする. そのままプログラム化すると

def factorial(N) {
  A = 1;
  for (I=1; I<=N; I++) A *= I;
  return A;
}

def e1(N) {
  E = 0;
  for ( I = 0; I <= N; I++ )
    E += 1/factorial(I);
  return E;
}

実はこの e1 関数はとても無駄が多い(何故か?) ので改良してみよう. $i! = i\cdot (i-1)!$ だから, 1/factorial(I) の分母を 1/factorial(I-1) から計算できる.

def e2(N) {
  F = 1;
  E = 1;     
  for ( I = 1; I <= N; I++ ) {
    F *= I;  
    E += 1/F; 
  }
  return E;
}

    

E = 1/0! F = I!
E = 1+1/1!+...+1/I!

実はこれでもまだ効率が無駄が多い. これは, 有理数計算特有の事情である. $a/b+c/d$ の計算には後の節で説明する整数 GCD の計算が必要になるが, $e(I-1)$ の分母は 明らかに $I!$ を割るので GCD 計算は無駄になる. よって, $e(I) = a(I)/I!$ とおいて, $a(I)$ の漸化式を求めよう. $e(I) = e(I-1)+1/I!$ より $a(I) = I\cdot a(I-1)+1$. よって, 次の プログラムが書ける.

def e3(N) {
  A = 1;
  for ( I = 1; I <= N; I++ )
    A = I*A+1;
  return A/factorial(N);
}

問題 6.2   三つのプログラムを実際に書いて, 結果, 計算時間を比較せよ.

[...] cputime(1);

を実行すると, 計算時間が表示されるようになる.

問題 6.3   $e(N) = N/D$ ($N$, $D$ は整数) と書けているとする.

• idiv(A,B)     :      A/B の整数部分を返す.
• nm(Q)     :      有理数 Q の分子を返す.
• dn(Q)     :      有理数 Q の分母を返す.

これらの組み込み関数を使って $e(N)$ の 10 進小数 展開を $K$ 桁求めよ. (小数点は不要. $K$ 桁の表示できればよい.) 例えば $e(10) = 9864101/3628800$ で, 10 桁求めると 2718281801.

問題 6.4  

$$\arctan x = \sum_{n=1}^\infty (-1)^{n-1} {x^{2n-1} \over {2n-1}}$$

と

$${\pi \over 4} = 4 \arctan {1 \over 5} - \arctan {1 \over 239}$$

(マチンの公式) を使って $\pi$ の有理数近似値を求める関数を書け.