| (15.1) |
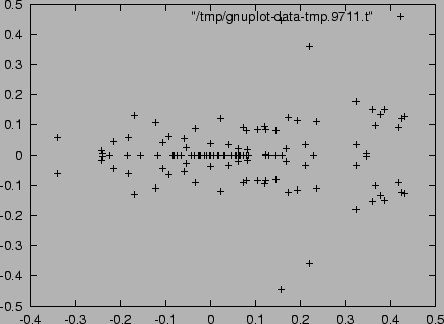
多変数の連立方程式系
![]() の
の ![]() 上のベクトル空間としての次元
上のベクトル空間としての次元 ![]() が
有限である場合,
が
有限である場合,
![]() を 0 次元イデアル
とよぶ.
根の多重度を適切に定義してやると
を 0 次元イデアル
とよぶ.
根の多重度を適切に定義してやると ![]() は連立方程式系
(16.1) の複素解の個数に一致することが知られている
([2, 5章2節 命題3, 3節 命題8]に多重度のない場合の証明がある).
は連立方程式系
(16.1) の複素解の個数に一致することが知られている
([2, 5章2節 命題3, 3節 命題8]に多重度のない場合の証明がある).
次の定理は 0 次元イデアルの定義とメンバシップアルゴリズム アルゴリズムを与えている定理 16.1 より容易に証明できる ([2, 5章3節 定理6]も参照).
また, この定理を, 辞書式順序の場合に適用すると, 次を得る.
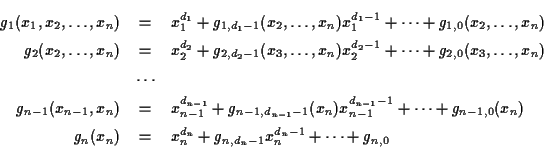
この例題の実験を行なう場合, ![]() をあまり大きくすると計算できない. せい
ぜい 4, 5程度にする. また, 次数も 2, 3 次程度にしておくこと. 辞書式順
序グレブナ基底は, いきなり gr などで計算しても大抵ムリなので,
Asir マニュアルをよく読んで, 上手な計算方法を学ぶこと.
実際にやってみればわかるように, 辞書式順序グレブナ基底は大変特徴
的な形をしている場合が多い:
をあまり大きくすると計算できない. せい
ぜい 4, 5程度にする. また, 次数も 2, 3 次程度にしておくこと. 辞書式順
序グレブナ基底は, いきなり gr などで計算しても大抵ムリなので,
Asir マニュアルをよく読んで, 上手な計算方法を学ぶこと.
実際にやってみればわかるように, 辞書式順序グレブナ基底は大変特徴
的な形をしている場合が多い:
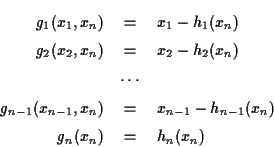
1 変数多項式の根は, pari(roots,Poly) で計算できる.
たとえば, pari(roots,x^3-1) で
![]() の(複素)近似根を計算できる.
ただし,
の(複素)近似根を計算できる.
ただし,
*** the PARI stack overflows ! current stack size: 65536 (0.062 Mbytes) [hint] you can increase GP stack with allocatemem()というようなエラーが出た場合には,
[295] pari(allocatemem,10^6)$などを実行して, pari の使用できるメモリを増やすこと.
[826] load("katsura");
1
[831] katsura(7);
[u0+2*u7+2*u6+2*u5+2*u4+2*u3+2*u2+2*u1-1,
2*u6*u0+2*u1*u7-u6+2*u1*u5+2*u2*u4+u3^2,
2*u5*u0+2*u2*u7+2*u1*u6-u5+2*u1*u4+2*u2*u3,
2*u4*u0+2*u3*u7+2*u2*u6+2*u1*u5-u4+2*u1*u3+u2^2,
2*u3*u0+2*u4*u7+2*u3*u6+2*u2*u5+2*u1*u4-u3+2*u1*u2,
2*u2*u0+2*u5*u7+2*u4*u6+2*u3*u5+2*u2*u4+2*u1*u3-u2+u1^2,
2*u1*u0+2*u6*u7+2*u5*u6+2*u4*u5+2*u3*u4+2*u2*u3+2*u1*u2-u1,
u0^2-u0+2*u7^2+2*u6^2+2*u5^2+2*u4^2+2*u3^2+2*u2^2+2*u1^2]