bash-2.03$ asir
This is Risa/Asir, Version 20000126.
Copyright (C) FUJITSU LABORATORIES LIMITED.
1994-1999. All rights reserved.
xm version 20000202. Copyright (C) OpenXM Developing Team. 2000.
ox_help(0); ox_help("keyword"); ox_grep("keyword"); for help message
Loading ~/.asirrc
[291] load("dsolv");
1
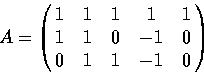
and
F = sm1_gkz( [ [[1,1,1,1,1],[1,1,0,-1,0],[0,1,1,-1,0]], [-1,0,0]])$
w = (1,1,1,1,0)
by using the Algorithm 2.3.14 of [1].
A = dsolv_starting_term(F[0],F[1],[1,1,1,1,0])$The output is as follows:
Computing the initial ideal.
Done.
Computing a primary ideal decomposition.
Primary ideal decomposition of the initial Frobenius ideal
to the direction [1,1,1,1,0] is
[[[x5+2*x4+x3+1, x5+3*x4-x2+1, x5+2*x4+x1+1,
3*x5^2+(8*x4+6)*x5+8*x4+3, x5^2+2*x5-8*x4^2+1, x5^3+3*x5^2+3*x5+1],
[x5+1,x4,x3,x2,x1]]]
----------- root is [ 0 0 0 0 -1 ]
----------- dual system is
[x5^2+(-3/4*x4-1/2*x3-1/4*x2-1/2*x1)*x5+1/8*x4^2
+(1/4*x3+1/4*x1)*x4+1/4*x2*x3-1/8*x2^2+1/4*x1*x2,
x4-2*x3+3*x2-2*x1,
x5-x3+x2-x1,
1]
A = map(myfctr,A[1][0]);
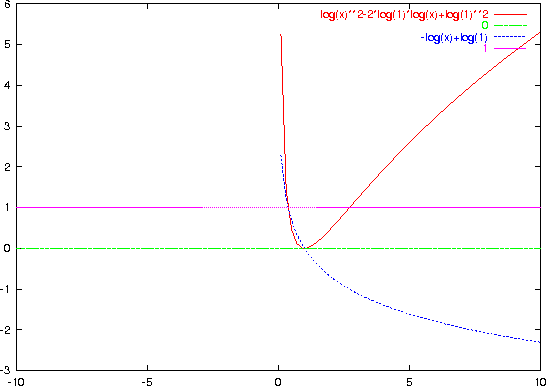
[[[1/8,1],[x5,-1],[log(x2)+log(x4)-2*log(x5),1],
[2*log(x1)-log(x2)+2*log(x3)+log(x4)-4*log(x5),1]],
[[1,1],[x5,-1],[-2*log(x1)+3*log(x2)-2*log(x3)+log(x4),1]],
[[1,1],[x5,-1],[-log(x1)+log(x2)-log(x3)+log(x5),1]],
[[1,1],[x5,-1]]]
B=map(subst,A,x1,x,x2,x,x3,x,x4,x,x5,1); /* Do not use t */ gnuplot_plot_function(B);