がなりたつ. ここで,
が成立していると仮定する.
証明:
![]() が
が ![]() ,
, ![]() の公約数なら,
の公約数なら,
![]() なので,
なので, ![]() は
は ![]() を割り切る.
また
を割り切る.
また ![]() も割り切る.
したがって,
も割り切る.
したがって, ![]() は
は ![]() と
と ![]() の公約数である.
の公約数である.
![]() が
が ![]() と
と ![]() の公約数なら,
同じ理由で,
の公約数なら,
同じ理由で, ![]() は
は ![]() と
と ![]() の公約数である.
の公約数である.
したがって, ![]() ,
, ![]() の公約数の集合と
の公約数の集合と
![]() ,
, ![]() の公約数の集合は等しい.
とくに GCD 同士も等しい.
証明おわり.
の公約数の集合は等しい.
とくに GCD 同士も等しい.
証明おわり.
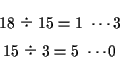
この GCD 計算方法をユークリッドの互除法という. プログラムに書くと次のようになる. 次の関数 e_gcd(A,B) は 数 A と数 B の GCD を互除法で求める.
def e_gcd(A,B) {
if (B>A) {
T = A; A = B; B=T;
}
while (B>0) {
R = A%B;
A=B; B=R;
}
return(A);
}
さてこのアルゴリズムの計算量を考察しよう.
命令 R = A%B が何回実行されるのか考えればよいであろう.
(最悪)計算量を求めるには, プログラムが最悪の振舞をする
データが何かわかれば計算量の評価ができる.
実は互除法での
最悪の場合のこの回数はフィボナッチ数列で実現できる.
次の漸化式
R = A%B の計算で終了したとする.
このとき,
証明:
![]() ,
, ![]() とおく.
互除法の各ステップにでてくる数を次のように
とおく.
互除法の各ステップにでてくる数を次のように
![]() ,
, ![]() とおく.
とおく.
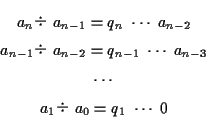
この証明により,
![]() ,
, ![]() に互除法を適用すると,
に互除法を適用すると,
![]() 回の
回の R = A%B の計算が必要なことも分る.
![]() の一般項を計算することにより,
次の定理が得られる.
の一般項を計算することにより,
次の定理が得られる.
上の結果により, 互除法による GCD 計算は素因数分解による GCD 計算に くらべ圧倒的に早いことがわかる.