




: 章末の問題
: ユークリッドの互除法とその計算量
: 互除法
目次
索引
整数 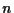 の素数判定には自明な方法がある.
の素数判定には自明な方法がある.
- 2, 3,
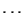 ,
, 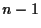 で割ってみる.
で割ってみる.
- 2, 3,
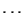 ,
,
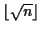 で割ってみる.
(
で割ってみる.
(
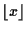 は
は 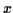 を越えない最大の整数.)
を越えない最大の整数.)
- 2 以外は奇数で割る.
いずれにせよ 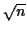 に比例する回数の割算が必要である. たとえば
に比例する回数の割算が必要である. たとえば
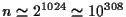 のとき,
のとき,
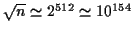 .
計算機では 1 クロックを単位として各種の命令が実行されている.
現在の一般的な CPU の
クロックは 1GHz (
.
計算機では 1 クロックを単位として各種の命令が実行されている.
現在の一般的な CPU の
クロックは 1GHz (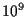 Hz) 程度, すなわち単位操作を一秒間に
Hz) 程度, すなわち単位操作を一秒間に
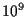 回できる程度なので, 1クロックで1回割算ができても
回できる程度なので, 1クロックで1回割算ができても
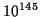 秒
秒
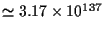 年程かかることになる.
年程かかることになる.
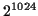 程度の数の素因数分解は, もっとよいアルゴリズム
を用いても困難であり, それが RSA 暗号の安全性の根拠となって
いる.
程度の数の素因数分解は, もっとよいアルゴリズム
を用いても困難であり, それが RSA 暗号の安全性の根拠となって
いる.
素朴には, 計算量とは, ある大きさのデータに対して, 計算にどれだけ
時間 (ステップ数) あるいは領域 (メモリ量) がかかるかを示す量である.
ここでいくつか曖昧な点がある.
この点をもうすこし詳しく考察しよう.
- データの大きさ
- 大きな数も小さな数も一つの数と見る
- メモリ上で必要な量を単位とする.
- 1 ステップとは
- 数の計算は 1 ステップと見る.
- 計算機の命令を 1 ステップと見る.
例えば浮動小数演算を用いる場合には, どちらで考えても同じだが,
近似なしに正確な値を有理数で求めていく場合には注意が必要である.
たとえば,
2 つの 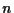 桁の整数
桁の整数
を筆算の要領で計算することを考える.
を使って, 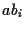 を計算してから
を計算してから 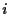 桁左にシフトしながら足して
行く. 一桁の数
桁左にシフトしながら足して
行く. 一桁の数 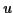 に対し
に対し
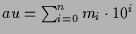 を計算するアルゴリズムは次の通り.
を計算するアルゴリズムは次の通り.
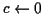
for ( 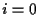 ;
; 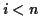 ;
; 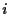 ++ )
++ )
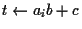
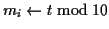
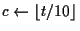
end for
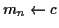
この計算で, かけ算は 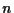 回, 10 による割算が
回, 10 による割算が 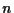 回必要である.
回必要である.
次に, 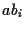 をシフトして足していく計算を考える.
これは, 繰り上がりを無視すれば
をシフトして足していく計算を考える.
これは, 繰り上がりを無視すれば 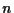 桁の数
桁の数
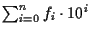 ,
,
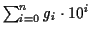 の加算と考えてよいから次のアルゴリズムで計算できる.
の加算と考えてよいから次のアルゴリズムで計算できる.
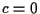
for ( 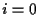 ;
; 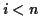 ;
; 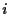 ++ )
++ )
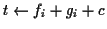
if 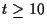
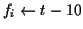 ,
, 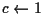
else 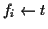 ,
, 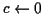
end for
(繰り上がりの処理)
これは, 本質的には加算が 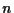 回で計算できる.
以上の計算が
回で計算できる.
以上の計算が 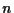 回必要になるから,
回必要になるから, 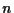 桁の数の積の計算には
桁の数の積の計算には
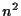 に比例するステップ数が必要になることが分かる.
に比例するステップ数が必要になることが分かる.
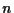 桁の整数を二つかける筆算アルゴリズムの計算量は
桁の整数を二つかける筆算アルゴリズムの計算量は 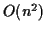 であった.
このアルゴリズムはさらに改良可能である.
簡単な高速化アルゴリズムとして, Karatsuba アルゴリズムを紹介する.
まず, 二桁の数
であった.
このアルゴリズムはさらに改良可能である.
簡単な高速化アルゴリズムとして, Karatsuba アルゴリズムを紹介する.
まず, 二桁の数
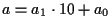
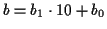 の積を考える.
普通にやると
の積を考える.
普通にやると
とかけ算が 4 回現れる. これを
と変形するとかけ算は 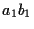 ,
, 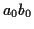 ,
,
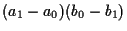 の 3 回になる. (加算は増える.)
これを繰り返す.
の 3 回になる. (加算は増える.)
これを繰り返す. 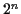 桁の整数
桁の整数 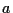 ,
, 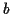 をかける場合
の計算量を
をかける場合
の計算量を 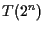 とする.
とする.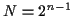 として
として
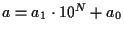 ,
,
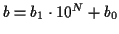 ,
,
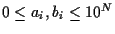 と書いて, 上の考察を適用する. 一桁の乗算, 加減算のコストをそれぞれ
と書いて, 上の考察を適用する. 一桁の乗算, 加減算のコストをそれぞれ
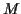 ,
, 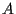 とすると,
とすると,
(第 2 項は「倍長」整数の加算コストを表す. 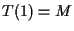 より,
この漸化式を解いて,
より,
この漸化式を解いて,
よって,
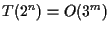 . これより
. これより
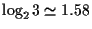 より
漸近的には筆算よりよいアルゴリズムと言える.
より
漸近的には筆算よりよいアルゴリズムと言える.
なお,
一変数多項式の積でも同じアルゴリズムが使える. かなり低い次数
(20 次程度) から, 通常の 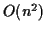 アルゴリズムより高速になる.
アルゴリズムより高速になる.





: 章末の問題
: ユークリッドの互除法とその計算量
: 互除法
目次
索引
Nobuki Takayama
平成15年9月12日
![]() の素数判定には自明な方法がある.
の素数判定には自明な方法がある.
![]() 程度の数の素因数分解は, もっとよいアルゴリズム
を用いても困難であり, それが RSA 暗号の安全性の根拠となって
いる.
程度の数の素因数分解は, もっとよいアルゴリズム
を用いても困難であり, それが RSA 暗号の安全性の根拠となって
いる.
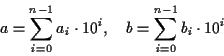
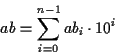
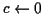
;
;
++ )
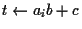
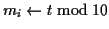
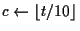
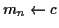
![]() 回, 10 による割算が
回, 10 による割算が ![]() 回必要である.
回必要である.
![]() をシフトして足していく計算を考える.
これは, 繰り上がりを無視すれば
をシフトして足していく計算を考える.
これは, 繰り上がりを無視すれば ![]() 桁の数
桁の数
![]() ,
,
![]() の加算と考えてよいから次のアルゴリズムで計算できる.
の加算と考えてよいから次のアルゴリズムで計算できる.
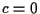
;
;
++ )
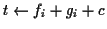
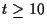
,
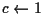
,
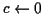
![]() 回で計算できる.
以上の計算が
回で計算できる.
以上の計算が ![]() 回必要になるから,
回必要になるから, ![]() 桁の数の積の計算には
桁の数の積の計算には
![]() に比例するステップ数が必要になることが分かる.
に比例するステップ数が必要になることが分かる.
![]() 桁の整数を二つかける筆算アルゴリズムの計算量は
桁の整数を二つかける筆算アルゴリズムの計算量は ![]() であった.
このアルゴリズムはさらに改良可能である.
簡単な高速化アルゴリズムとして, Karatsuba アルゴリズムを紹介する.
まず, 二桁の数
であった.
このアルゴリズムはさらに改良可能である.
簡単な高速化アルゴリズムとして, Karatsuba アルゴリズムを紹介する.
まず, 二桁の数
![]()
![]() の積を考える.
普通にやると
の積を考える.
普通にやると
![]() アルゴリズムより高速になる.
アルゴリズムより高速になる.